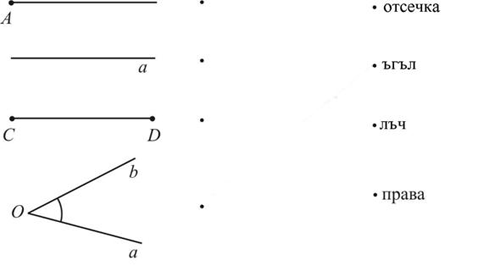PRAVILNIK O PROGRAMU ZAVRŠNOG ISPITA U OSNOVNOM OBRAZOVANJU I VASPITANJU("Sl. glasnik RS - Prosvetni glasnik", br. 1/2011, 1/2012, 1/2014, 12/2014, 2/2018, 3/2021, 14/2022, 4/2023 i 5/2023 - ispr.) |
Образователни стандарти за край на задължителното основно образование по математика с примерни задачи
МА.1.1.1. Ученикът умее да прочете и да запише различни видове числа (естествени, цели, рационални).
Задача |
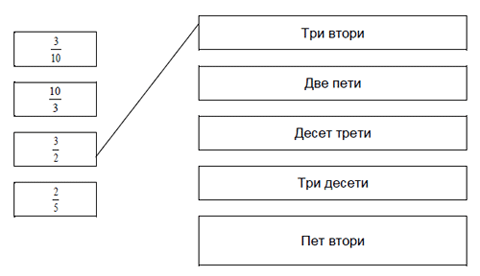
Свържете равните числа, както е посочено:
|
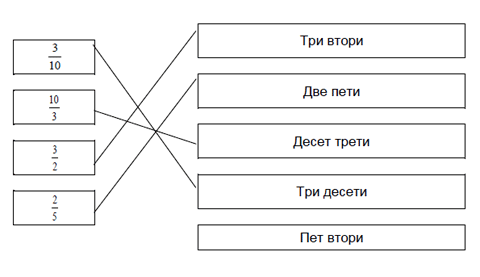
Решение |
|
|
МА. 1.1.2. Ученикът умее да преобразува число от десетична в обикновена дроб и обратно.
Задача |
||||||||||||||||||||
Кое от дадените числа е равно на числото 0,3? Посочете верния отговор:
|
||||||||||||||||||||
Решение |
||||||||||||||||||||
|
МА.1.1.3. Ученикът умее да сравнява по големина числа от един и същ запис, помагайки се с чертеж, когато е необходимо.
Задача |
||||||||||||||||||
Дадени са числата:
Кое от посочените числа е
|
||||||||||||||||||
Решение |
||||||||||||||||||
|
МА.1.1.4. Ученикът извършва основни действия с числа от един и същ запис, помагайки се с чертеж, когато е това необходимо, (в случай на събиране и изваждане на дроби, с един и същ знаменател), пресмята например 1/5 от n, където nе дадено естествено число.
Задача |
Изчислете и запишете верния отговор: a) - 6 : 2 = ________ б) - 6 - 2 = ________ в) - 6 ∙ 2 = ________ г) - 6 + 2 = ________ |
Решение |
a) - 6 : 2 = -3 б) - 6 - 2 = -8 в) - 6 ∙ 2 = -12 г) - 6 + 2 = -4
|
МА.1.1.5. Ученикът умее да дели с остатък, като делителят е едноцифрено число, и знае кога някое число е делимо на друго.
Задача |
|||||||||||||||
Попълнете следната таблица, както е започнато:
|
|||||||||||||||
Решение |
|||||||||||||||
|
MA.1.1.6. Ученикът умее да използва цели числа и прости изрази с тях, помагайки си с визуални въображения.
Задача |
Днес е рожденият ден на Йована. Тя казва: "След три години ще съм навършила 18 години". На колко години е Йована сега? Посочете верния отговор. а) 12 |
Решение |
б) 15 |
МА.1.2.1. Ученикът извършва формални действия, които са редуцирани и са зависими од интерпретацията им; умее да реши линейно уравнение, в което неизвестната се явява само в един член.
Задача |
Кое число е решение на уравнението x/2 + 2 = 8? Посочете верния отговор: а) 5 б) 6 в) 12 г) 20 |
Решение |
в) 12 |
МА.1.2.2. Ученикът умее да извършва определени операции, които са съкратени в зависимост от интерпретацията им и умее да вдига дадено число на степен, знае основните действия със степени.
Задача |
Произведението 210·22 е равно на: Посочете верния отговор: а) 25 б) 28 в) 212 г) 220
|
Решение |
в) 212 |
Задача |
Посочете верния отговор: Стойността на степена 0,32 е: а) 0,06 |
Решение |
в) 0,09 |
МА.1.2.3. Ученикът умее да извършва определени операции, които са съкратени и зависят от интерпретацията им, умее да събира, изважда и умножава едночлени.
Задача |
Опростете следния израз: 5a3 + 7a3 = _____ 9x2 - 4x2 = _____ 2b · 3b2 = _____ |
Решение |
5a3 + 7a3 = 12a3 9x2 - 4x2 = 5x2 2b · 3b2 = 6b3 |
МА.1.2.4. Ученикът умее да извършва определени операции, които са съкратени и зависят от интерпретацията им; определя стойността на определена функция, зададена таблично или с формула.
Задача |
||||||||
Функцията е дадена с формула y = 2x + 1. Определете съответните стойности на променливите х и y и попълнете таблицата.
|
||||||||
Решение |
||||||||
|
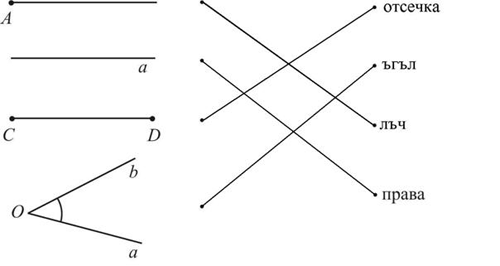
МА.1.3.1. Ученикът владее с понятията: отсечка,лъч,права,равнина и ъгъл (забелязва техни те модели в реалните ситуации и умее да ги начертае, използвайки пособия; разпознава някои видове ъгли и успоредни и перпендикулярни прави).
Задача |
Свържете чертежа с названието на фигурата представена на този чертеж.
|
Решение |
|
|
МА.1.3.2. Ученикът владее понятията: триъгълник, четириъгълник, квадрат и правоъгълник (забелязва техните модели в реални условия и умее да ги начертае използвайки пособия; разпознава основните видове триъгълници, знае основните елементи на триъгълник и умее да пресмята обиколка и лице на триъгълник, квадрат и правоъгълник, въз основа на елементите, които са непосредствено дадени в условието на задачата; умее да намери неизвестна страна на правоъгълния триъгълник, като прилага Питагоровата теорема).
Задача |
||||
Изчислете лицето на пода, покрито с килим дълъг 3,5 mи широк 2 m. посочете верния отговор:
|
||||
Решение |
||||
б) 7 m2 |
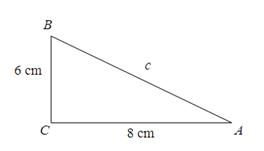
Задача |
||
c = _____ |
||
Решение |
||
c = 10 cm |
МА.1.3.3.Ученкът владее понятията: кръг, окръжност (изтъква техните основни елементи, забелязва техните модели в реални условия и умее да ги начертае, ползвайки чертежно пособие; умее да пресметне периметър на окръжност и лице на кръг с даден радиус).
Задача |
Колко е периметърът на окръжност, чийто радиус е 7 cm? а) 14 cm б) 49 cm в) 14π cm г) 49π cm |
Решение |
в) 14 π cm |
МА.1.3.4.Ученикът е овладял понятията: куб и правоъгълен паралелепипед (забелязва техните модели в реални условия, знае техните основни елементи и изчислява поврхнината и обема им).
Задача |
||
Повърхнината на призмата е______cm2. |
||
Решение |
||
Р= 2·36 cm2+ 4·60 cm2= 72 cm2+ 240 cm2= 312 cm2 Повърхнината на призмата е 312 cm2. |
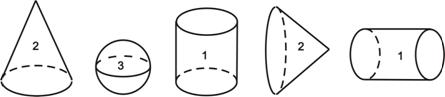
МА.1.3.5. Ученикът владее понятията:конус,цилиндър и кълбо (забелязва техните модели в реални условия, знае техните основни елементи).
Задача |
Върху всеки цилиндър напишете числото 1,върху всеки конус напишете числото 2, а върху всяко кълбо числото 3.
|
Решение |
|
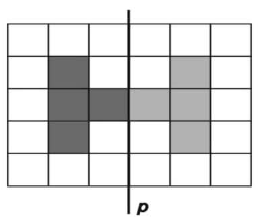
МА.1.3.6. Ученикът интуитивно разбира понятието еднаквост на равнинни фигури (които могат да съвпадат при някое движение).
Задача |
||||||
|
||||||
Решение |
||||||
в) |
Задача |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Дадена е фигурата F. Оцветете необходимите квадратчета така, че фигурата Gда е еднаква (да може да съвпада) с фигурата F.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Решение |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
МА.1.4.1. Ученикът умее да използва оподходящи единици за дължина, лице, обем, маса, време и големина на ъгъл.
Задача |
|||||||||||||||
Попълнете празните полета на таблицата с необходимата мерна единица:
|
|||||||||||||||
Решение |
|||||||||||||||
|
МА.1.4.2.Ученикът умее да преобразува по-големи мерни единици за дължина, маса и време в по-малки.
Задача |
Кой период от време е най-дългият? Посочете верния отговор |
Решение |
б) 100 дни |
МА.1.4.3. Ученикът умее да използва парични знаци с различна стойност.
Задача |
Ако развалиш 3 банкноти от по 200 динара на банкноти по 50 динара, колко банкноти ще получиш? Ще получа______банкноти от 50 динара. |
Решение |
Ще получа 12 банкноти от 50 динара. |
МА.1.4.4. Ученикът умее да избира подходяща мерна единица при измерване; закъргля величини, представени с дадена мярка.
Задача |
||||||||||||||||||
В празните полета поставете подходящите мерни единици: km, cm, l, kgили g.
|
||||||||||||||||||
Решение |
||||||||||||||||||
|
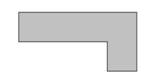
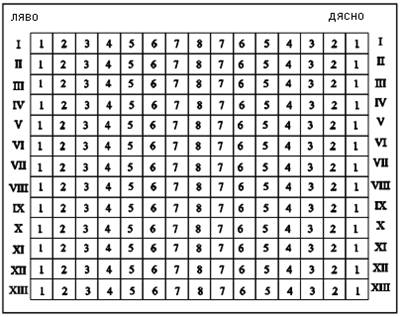
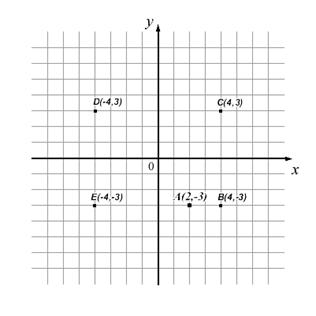
МА.1.5.1. Ученикът умее да изрази поло жението на някой обект като го слага в редове и колонки; да построи точка в първия квадрант на координатната система, когато са дадени координатите й и обратно.
Задача |
На чертежа е даден план на кино ОДЕОН. Марко е купил билет в шестия ред ляво и седалка 3. Оцветете седалката на Марко.
|
Решение |
|
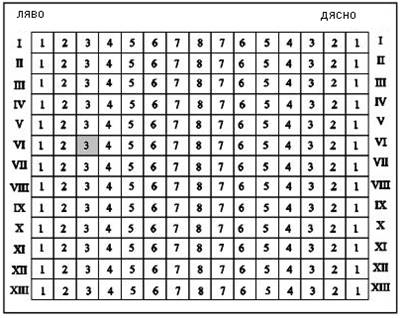
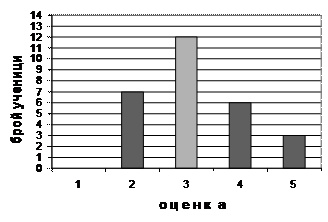
МА.1.5.2. Ученикът умее да разчита и разбира данните от графика, диаграма или от таблица и определя минималната и максималната стойност на зависимата променлива.
Задача |
Числото на слънчевите дни в една година, по отделни месеци, е дадено с диаграма: |
а) Най-малко слънчеви дни през годината е имало през месец-----------. |
Решение |
а) Най-малко слънчеви дни през годината е имало през месец декември. б) Най-много слънчеви дни през годината е имало през месец август |
МА.1.5.3. Ученикът умее да представя данни от таблицата с графика и обратно.
Задача |
||||||||||||
Използвайки данните за успеха на учениците от класната работа, представени в таблицата, завършете графиката по начина, по който е започната:
|
||||||||||||
Решение |
||||||||||||
|
||||||||||||
МА.1.5.4. Ученикът умее да пресмята процент от дадено число.
Задача |
Милена решава да си купи маратонки на цена от 4 000 динара. При покупката продавача й дава отстъпка от 10%. Изчислете отстъпката в динари? Милена получава отстъпка ______ динара. |
Решение |
Милена получава отстъпка 400 динара. |
МА.2.1.1. Ученикът умее да сравнява по големина числа от различен вид.
Задача |
||||
Дадени са следните числа:
Кое от посочените числа е най-малко, а кое най-голямо? |
||||
Решение |
||||
Най-малкото число е -1,2, а най-голямото 1½. |
МА.2.1.2.Ученикът умее да определя обратно число, реципрочна стойност и абсолютна стойност на число; изчислява стойност на прости изрази с повече действия с различни приоритети, включително и разкриване на скоби с числа от един и същ запис.
Задача |
Изчислете: а) (3/4 - 1/2) • 4 = б) 3,2 · (4,3 +5,7) = |
Решение |
а) (3/4 - 1/2) • 4 = 1 б) 3,2 · (4,3 +5,7) = 32 |
Задача |
|||||||||||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||||||||
Решение |
|||||||||||||||||||||||||||||||||||||||||
|
МА.2.1.3. Ученикът умее да прилага основните признаци на делимост с 2, 3, 5, 9 и десетични единици.
Задача |
|||||||||||||||
Свържи дадените числа с подходящите изречения:
|
|||||||||||||||
Решение |
|||||||||||||||
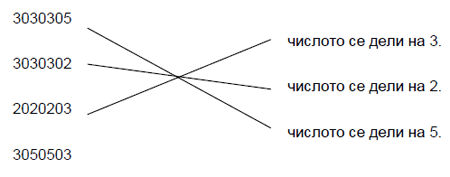 |
МА.2.1.4. Ученикът умее да използва числа и числови изрази в обикновени реални условия.
Задача |
За 25 тетрадки е заплатено 750 динара. Тетрадката е за 20 динара по -скъпа от молива. За 750 динара могат да се купят _ молива. |
Решение |
750 : 25 = 30 За 750 динара могат да се купят 75 молива. |
МА.2.2.1. Ученикът е довел до солидно равнище на упражненост операциите с многочлени и числа; умее да решава линейно уравнение и система от две линейни уравнения с две неизвестни.
Задача |
Посочете верния отговор. Коренът на уравнението а) -20 и -10 б) -10 и 10 в) 10 и 20 г) 20 и 30 |
Решение |
в) 10 и 20 |
МА.2.2.2. Ученикът е в действията с числа достигнал солидно равнище на упражненост, умее да работи със степени и знае какво е квадратен корен.
Задача |
||||||||||||
При правилно твърдение отбележете думата ВЯРНО, а при неправилно думата НЕВЯРНО.
|
||||||||||||
Решение |
||||||||||||
|
МА.2.2.3. Ученикът е в аритметичните действия достигнал солидно равнище на упражненост; умее да събира и изважда многочлени, умножава два двучлена и да повдигне на квадрат двучлен.
Задача |
|||||||||||||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||||||||||
Решение |
|||||||||||||||||||||||||||||||||||||||||||
|
МА.2.2.4. Ученикът е в аритметичните действия достигнал солидно равнище на упражненост; умее да забелязва зависимостта между две променливи величини, знае функцията y = a · x и интерпретира нейните свойства с графика; свързва с тях понятието права пропорционалност и определя неизвестния член на пропорцията.
Задача |
||||
На един от дадените чертежи графично е представена зависимостта между количеството на оловото (х) и цинка (у) в сплава, където се оловото и цинка намират в отношение 2:1.
|
||||
Решение |
||||
в) |
Задача |
За 8 mплатно трябва да се заплати 2 400 динара. a) Колко струва 12 mот това платно? а) 12 mплатно струва _______ динара. |
Решение |
а) 12 mплатно струва 3 600 динара. |
МА.2.2.5. Ученикът е достигнал солидно равнище на упражненост в действията с числа, умее да използва уравнение за решаване на прости текстови задачи.
Задача |
Петър харчи една трета от спестените си пари за купуване на ваучер за мобилния си телефон, след което му остават 800 динара. Каква е била спестената сума пари на Петър? Спестената сума пари на Петър е била ________динара. |
Решение |
Спестената сума пари на Петър е била 1200 динара. |
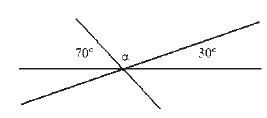
МА.2.3.1. Ученикът умеeда определи съответни и прилежащи ъгли, съседни и противоположни ъгли; смята с тях, ако са дадени в цели градуси.
Задача |
Определете ъгъла α от чертежа:
|
Решение |
α = 80° |
МА.2.3.2. Ученикът умеeда определя връзката между страните и ъглите в триъгълника, сбора на ъглите в триъгълника и четириъгълника и решава задачи, прилагайки Питагоровата теорема.
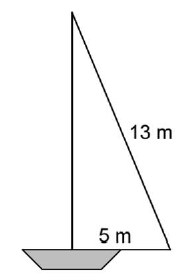
Задача |
||||
Пресметнете лицето на платното на кораба од чертежа.
Лицето на платното е:________ m2. |
||||
Решение |
||||
Ако височината на платното е x, тогава е x2 = 132 - 52 = 169 - 25 = 144.
Лицето на платното е 30 m2. |
МА.2.3.3. Ученикът умее да използва формулите за изчисляване на периметър на окръжност и лице на кръг и кръгов пръстен.
Задача |
Лицето на малкия кръг е 9π cm2. Лицето на кръговия пръстен е 16π cm2.
Радиуса на по-голямия кръг е ____ cm. |
Решение |
Pvk = (9π + 16π) cm2 = 25π cm2 Радиуса на по-голямия кръг е 5 cm. |
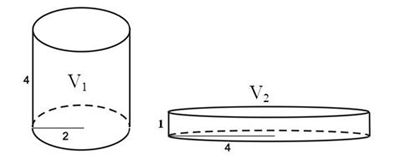
МА.2.3.5. Ученикът умее да изчислява повърхнина и обем на цилиндър, конус и кълбо, когато необходимите елементи са непосредствено дадени в задачата.
Задача |
На чертежа се посочват два цилиндъра с обеми V1 и V2.
Посочете верния отговор. а) V1 > V2 б) V1 < V2 в) V1 = V2 |
Решение |
в) V1 = V2 |
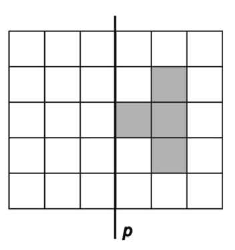
МА.2.3.6. Ученикът умее да забелязва фигури с осева симетрия и определя оста на симетрия; използва еднаквостта и ясвързва с характерните свойства на фигурите (напр. успоредност и равност на страни на успоредник).
Задача |
Защриховайте четири полета на чертежа, така че да получите осево- симетрична фигура спрямо правата p.
|
Решение |
|
МА.2.4.1. Ученикът умее да сравнява величини, представени с различни мерни единици за дължина и маса.
Задача |
||||||||||||||
Учителката е написала на дъската масата на четири предмета. Отбележи буквата под предмета който е най-тежък.
|
||||||||||||||
Решение |
||||||||||||||
|
Задача |
Продавача има в магазина три очистени пилета чиито маси са 1340 g, 1,35 kg, и 1kg 290 g. Подреди тези маси по големина, от най-голямата до най-малката. Отговор: ________ > _________ > ________ |
Решение |
1,35 kg > 1340 g > 1kg 290 g |
МА.2.4.2. Ученикът умее да преобразява стойност на една валута в друга, като съставя правилно съответната пропорция.
Задача |
Новогодишните празници Мая прекарва в Италия. Пътят и пребиваването й там струва 200 евро. Каква стойност в динари е заплатила Мая, ако в деня на плащането едно евро е струвало 105 динара? Мая е заплатила___________ динара. |
Решение |
Мая е заплатила 21 000 динара. |
Задача |
Ако една норвежка крона струва 12,50 динара, а едно евро 105 динара, колко струват 10 евро, превърнати в норвежки крони? 10 евро струват__________ норвежки крони. |
Решение |
10 евро е 105 ·10 =1050 динара. 1050: 12,5 = 84 |
МА.2.4.3. Ученикът умее да изразява дадена величина с приблизителна стойност.
Задача |
||||||||
Цветарят трябва да закръгли цените на вносните цветя до най-близките цели числа. Напишете новите им цени.
|
||||||||
Решение |
||||||||
|
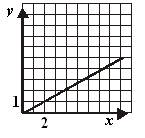
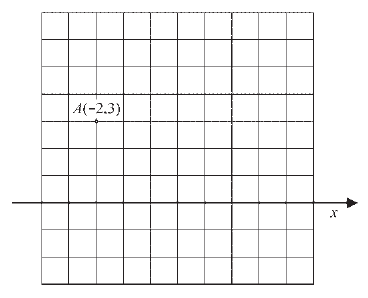
МА.2.5.1. Ученикът владее с описание на координатната система (определя координати на точки, както и на осево или централно- симетрични и тн.).
Задача |
Въз основа на дадените координати на точката А начертайте остта yв правоъгълната Декартова координатна система.
|
Решение |
|
МА.2.5.2. Ученикът умее да разчита по-прости диаграми и таблици и въз основа на това ги обработва по даден критерий (например намира средно аритметично за дадено множество данни, сравнява стойности на образцови данни със средната стойност).
Задача |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
В таблицата са дадени разстоянията между градовете изразени в километри.
Въз основа на таблицата довършете следните изречения, така да е точно твърдението: а) Разстоянието между Чачак и Никшич е _______ километъра. б) Разстоянието между Никшич и ______________ е също както и разстоянието между Никшич и ________________. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Решение |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
а) Разстоянието между Чачак и Никшич е 395 километара. б) Разстоянието между Никшич и Нови Сад е също както и разстоянието между Никшич и Зренянин. |
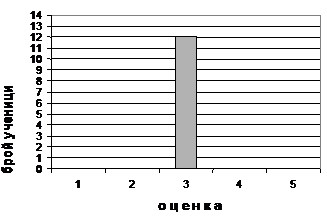
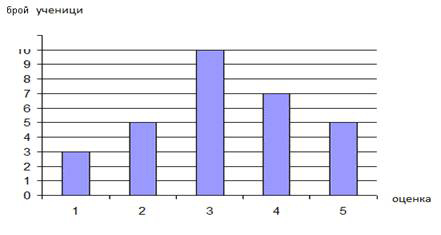
МА.2.5.3. Ученикът умее да обработва събраните данни и да ги представи в таблица или графично; умее да намери средната стойност с медиана.
Задача |
||||||||||||||||
Да дена е диаграма за успеха на учениците в една паралелка на тест по математика.
а) Допълнете таблицата, която съответства на посочената диаграма, както е започнато.
б) Изчислете средната белешка на теста по математика Средната белешка на теста по математика е ________ |
||||||||||||||||
Решение
Средната белешка на теста по математика е 3,2 |
||||||||||||||||
МА.3.1.2. Ученикът оперира с понятието "делимост" в по-сложни ситуации.
Задача |
Напишете три числа в петата хиляда, чиято цифра на десетици е 2, а които са делими на 9. Това са числата_______, ________, ________. |
Решение |
Които и да е написани три числа от множеството{4023, 4122, 4221, 4320, 4329, 4428, 4527, 4626, 4725, 4824, 4923}. |
МА.3.1.3. Ученикът умее да използва числа и числови изрази в реални условия.
Задача |
Цветарка прави и продава букети цветя. Всеки букет се състои от 4 рози и 3 маргаритки. Цветарката трябва да продаде най-малко ______ букета. |
Решение |
Печалбата й от един букет е: 4·35 + 3·25+ 60= 140 + 75 + 60 = 275 |
МА.3.2.2.Ученикът е достигнал високо равнище на упражненост при извършване на действия с числа, с изтъкване на използваните свойства, умее да използва свойствата на степен и квадратичен корен.
Задача |
Ако е познато, че 322= 1024, изчислете: а) √10,24 = ______________ б) √102400 = _____________ в) √0,1024 = ______________
|
Решение |
а) √10,24 = 3,2 б) √102400 = 320 в) √0,1024 = 0,32
|
МА.3.2.3. Ученикът е достигнал високо равнище на упражненост при извършване на действия с числа, с изтъкване на използваните свойства, умее да прилага формулите за съкратено умножение, упражнено преобразува изрази и свежда ги до опростена форма.
Задача |
Посочете верния отговор: Многочленът (а - 1)(2а + 1) - (а - 6)(а + 6) е равен на многочлена: a) а2 - а + 35 б) а2 - а - 37 в) а2 + 35 г) а2 - 37 |
Решение |
а) а2 - а + 35 |
Задача |
Изчисли: а) разликата на квадратите на числата 7 и 3: __________________________________ б) квадрата на разликата на числата 7 и 3: ___________________________________ в) сбора от квадратите на числата 7 и 3: ___________________________________ г) квадрата на сбора на числата 7 и 3: ______________________________________ |
Решение |
а) 72 - 32 = 49 - 9 = 40 б) (7 - 3)2 = 42 = 16 в) 72 + 32 = 49 + 9 = 58 г) (7 + 3)2 = 102 = 100 |
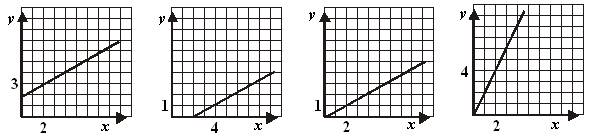
МА.3.2.4. Ученикът е достигнал високо равнище на упражненост при извършване на действията с числа, с истъкване на свойствата, които се исползват; умее да разграничава право и обратно пропорционални величини и това изразява с подходящ запис; знае линейната функция и знае с графикaда интерпретира нейните свойства.
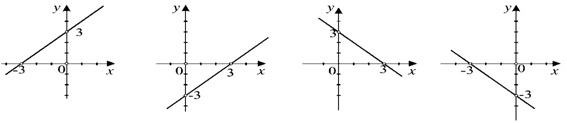
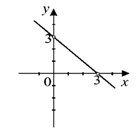
Задача |
||||||||
Кой от следните графици е график на функцията y = -x + 3 ?
|
||||||||
Решение |
||||||||
|
||||||||
Задача |
Деветима приятели могат да почистват басейн за 4 дена. Още колко приятели трябва да им помогнат за да басейна бъде поч истен за 3 дена? Басейна ще бъде очистен за 3 дена ако им помогнат още _________приятели. |
Решение |
9 : x = 3 : 4 или x : 9 = 4 : 3 |
МА.3.2.5.Ученикът е достигнал високо равнище на упражненост при вршене на операции със истъкване на свойства, които се прилагат, знае да исползва уравнения, неравенства и системи уравнения, решавайки по-сложни текстови задачи.
Задача |
Докато е била на лятна почивка Надя се е на всеки от своите 9 приятели от блока обадила с писмо или поштенска картичка. Марките за поштенските картички е плащала по 10 динари, а марки за писмо по 15 динари. Колко писма и колко картички е испратила Надя, ако е исрасходвала за марки общо 110 динари? Решението да се даде с неговата обосновка. Надя е испратила ______писма и ________ картички. |
Решение |
х - число на писмата Решение на системата е x = 5 и y = 4, без значение на метода на решаване. Надя е испратила 5 писма и 4 картички. |
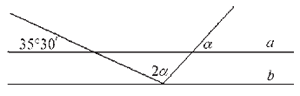
МА.3.3.1.Ученикът умее да изчислява ъгли, включвайки и преобразуване на мерните единици за големина на ъгъл; прави изводи, като използва признаците на успоредни и перпендикулярни прави, включвайки и ъгли, които образуват прави, пресичащи се в равнината.
Задача |
Ако правеите a и b са успоредни, определете мярката на ъгъла α.
гълът е α =____ |
Решение |
Ъгълът е α =48°10΄ |
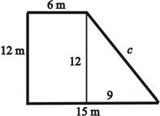
МА.3.3.2. Ученикът умее да използва основните свойства на триъгълник, четириъгълник, успоредник и трапец, пресмята техните обиколки и лица въз основа на елементите, които не са непосредствено дадени в условието на задачата, умее да ги конструира.
Задача |
||
Колко метъра жица eнеобходимо за oграждане на двор с форма на правоъгълен трапец, както е представено на чертежа? Необходимо е решение с неговата обосновка. Трябва _____ метъра жица. |
||
Решение |
||
Трябва 48 метъра жица. |
МА.3.3.3. Ученикът умее да забелязва централен и периферен ъгъл, да изчислява лице на кръгов сегмент, както и дължина на дъга от окръжност.
Задача |
Ако хордата AB е равна на радиуса на кръга, пресметнете големината на ъгъла ACB.
∠ABC = ____________
|
Решение |
∠ABC = 30° |
Задача |
Колко пъти лицето на кръговия сегмент с съответстващ централен ъгъл 30о е по-малко от лицето на целия кръг?
По-малко е ____ пъти. |
Решение |
По-малко е 12 пъти. |
МА.3.3.4. Ученикът умее да изчислява повърхнина и обем на призма и пирамида, включвайки и случаи, когато необходимите елементи не са непосредствено дадени.
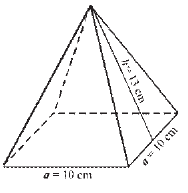
Задача |
||||||||||||||
Пресметнете обема на правилна четириъгълна пирамида, ако основният й ръб е a = 10 cm, а апотемата й - h = 13cm.
Обемът на пирамидата е _____cm3. |
||||||||||||||
Решение |
||||||||||||||
Обемът на пирамидата е 400 cm3. |
МА.3.3.5.Ученикът умее да изчислява повърхнина и обем на цилиндър, конус и кълбо, включвайки и случаи, когато необходимите елементи не са непосредствено дадени.
Задача |
Правоъгълен триъгълник, чиито катети са а = 9 cm, b = 12 cm, ротира около катета b. а) 1: 1 |
Решение |
в) 3: 5 |
Задача |
Колко е повърхнината на най-голямото кълбо което може да се сложи в кутия с форма на куб, чийто ръб е 20 cm?
Лицето на кълбото е ____ цм. |
Решение |
Повърхнината на кълбото е 400π цм2. |
МА.3.3.6. Ученикът умее да прилага еднаквост и подобност на триъгълници, свързвайки по този начин разни свойства на равнинните фигури.
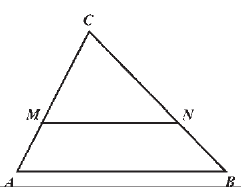
Задача |
||
Отсечките MN и АВ са успоредни. Ако е MN: AB= 2: 3, изчисли СМ: MА?
|
||
Решение |
||
а) 2: 1 |
Задача |
||||||||||||
При точното твърдение отбележете думата ВЯРНО,а при неточното твърдение думата НЕВЯРНО.
|
||||||||||||
Решение |
||||||||||||
|
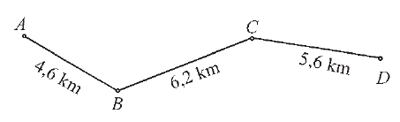
МА.3.4.2. Ученикът умее да извършва преценка, да закръгля дадените данни и да изчислява с приблизителните им стойности; умее да определя големината на грешката (например, по-малко от 1 динар, 1 см и 1 г).
Задача |
Разстоянието между точките А и Dе представено със следния чертеж
Мира е определила разстоянието между точките А и D, след като е закръглила всяко едно от дадените разстояния на цяло число км и извършила тяхното събиране. Вяра най-напред е събрала разстоянията от посочения чертеж и е закръглила получената сума на най-близкото цяло число км. |
Решение |
а) Мира получава по-голямо число от Вяра. |
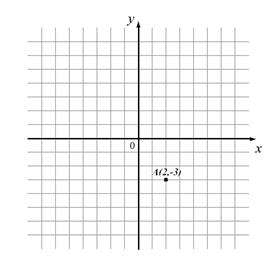
МА.3.5.1. Ученикът умее да определи положението (координатите) на точки, които изпълн яват по-сложни условия.
Задача |
Начертай в координатната система всичките точки които са на равни растояния от оста xкакто и точката А, а на които растоянието од остта y е двапъти по-голямо од растоянието на точката A от остта y.
|
Решение |
|
МА.3.5.2. Ученикът умее да разчита диаграми и таблици.
|
Задача |
||||||||||||||||||||||||||||||||||||||||||||||||
В таблицата са дадени разстояниата между някои градове в километри.
а) Кой град сe на 115 km разстояние?....................... б) Кои два града от Белград 353 km?............................................... в) Кои два града се намират на разстояние по-малко от 50 km?....................................... г) Колко градове в таблицата са на разстояние повече от 200 kmот Белград?................... |
||||||||||||||||||||||||||||||||||||||||||||||||
Решение |
||||||||||||||||||||||||||||||||||||||||||||||||
а) Крагуевац б) Кралево и Суботица в) Яагодина и Крагуевац г) три |
МА.3.5.3. Ученикът умее да събира и обработва данни, съставя сам диаграма или таблица, изобразява графично взаимоотношение между величини.
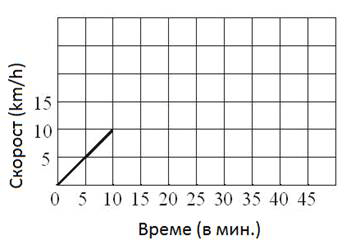
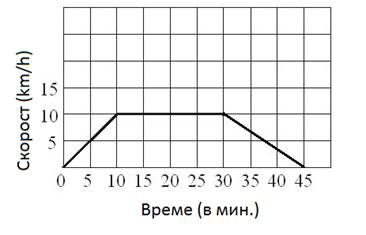
Задача |
Мая кара колело 45 минути. След първите 10 минути колоездене достига скорост от 10km / h. С тази скорост кара следващите 20 минути, след което започва равномерно да намалява скоростта до спиране. Попълнете диаграмата, представляваща колоезденето на Мая.
|
Решение |
|
МА.3.5.4. Ученикът умее да прилага процентното изчисление в по-сложни ситуации.
Задача |
Цената на книгата е първоначално увеличена с 10%, след това е намалена с 10% и сега е 198 динара. Каква е била цената на книгата преди поскъпването й? Посочете верния отговор. а) 198 динара |
Решение |
б) 200 динара |
Образователни стандарти за край на задължителното основно образование по математика с непознати задачи с цел проверка
МА.2.3.4. Ученикът владее понятията призма и пирамида, иачислява тяхната поврхнина и обем, когато в задачата непосредствено са дадени необходимите елементи.
Задача |
|||||||||||||||||||||
Дължината на основния ръб на правилна триъгълна еднакворъбеста пирамида е 8 cm. Колко е нейната повърхнина? Повърхнината на пирамидата е _______cm2. |
|||||||||||||||||||||
Решение |
|||||||||||||||||||||
P = a2 Ö3 , P = 82 Ö3 P = 64 Ö3 cm2 Повърхнината на пирамидата е 64 Ö3 cm2. |
М.А.2.5.4. Ученикът умее да прилага процентно изчисление в прости реални условия (например, промяна на цена на даден артикул с определен процент).
Задача |
Гордана продава сладолед. На всеки продаден сладолед на цена от 60 динара тя печели 6 динара. Каква е процентната й печалба от един продаден сладолед? Посочете верния отговор. а) 6% |
Решение |
г) 10% |
МА.3.1.1. Ученикът умее да определя числовата стойност на по-сложни изрази.
Задача |
|||||||||||
Пресметнете произведението на изразите А и В, ако е А = _______, B= ______ , произведението е A· B= _______ |
|||||||||||
Решение |
|||||||||||
|
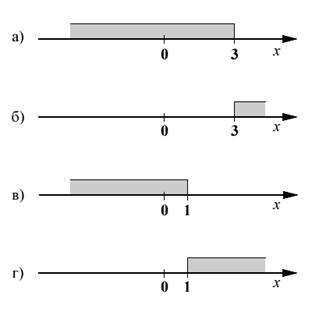
МА.3.2.1. Ученикът е достигнал високо равнище на упражненост при извършване на действия, изтъквайки приложените свойства; знае да съставя и решава линейни уравнения и неравенства и системи от линейни уравнения с две неизвестни.
Задача |
||||||||||
Кое множество от числа, представено на числовата ос, е решение на неравенството:
|
||||||||||
Решение |
||||||||||
|
МА. 3.4.1. Ученикът умее да преобразува мерните единици и да изчислява с тях, когато е наобходимо.
Задача |
В киното филмът свършва в 22 часа и 10 минути. Кога е започнал филмът, ако той е бил с продължителност от 115 минути? |
Решение |
в) 20 часа и 15 минути |